Post-Quantum Verifiable Credentials
Carlo Sanna (Politecnico di Torino)
12/09/2024
Verifiable Credentials
Verifiable Credentials (VCs) are digital credentials designed to represent information that would otherwise be stored in physical credentials, such as passports, driving licences, university degrees, subscriptions to a service, etc. Thanks to the use of cryptography, VCs have several advantages over their physical counterparts. In particular, they are tamper-resistant, privacy-respecting, and machine-verifiable in a decentralized way. VCs are defined in the Verifiable Credentials Data Model of the World Wide Web Consortium open standards [1].
VCs are the top layer (Layer 3) of the Self-Sovereign Identity (SSI) reference model; see Figure 1. Layer 1 is used to store information about public identities and is implemented by a Verifiable Data Registry (VDR), while Layer 2 is used to initiate peer authentication and employs Decentralized Identifiers (DIDs) – in this blog post, we will not focus on these two layers.
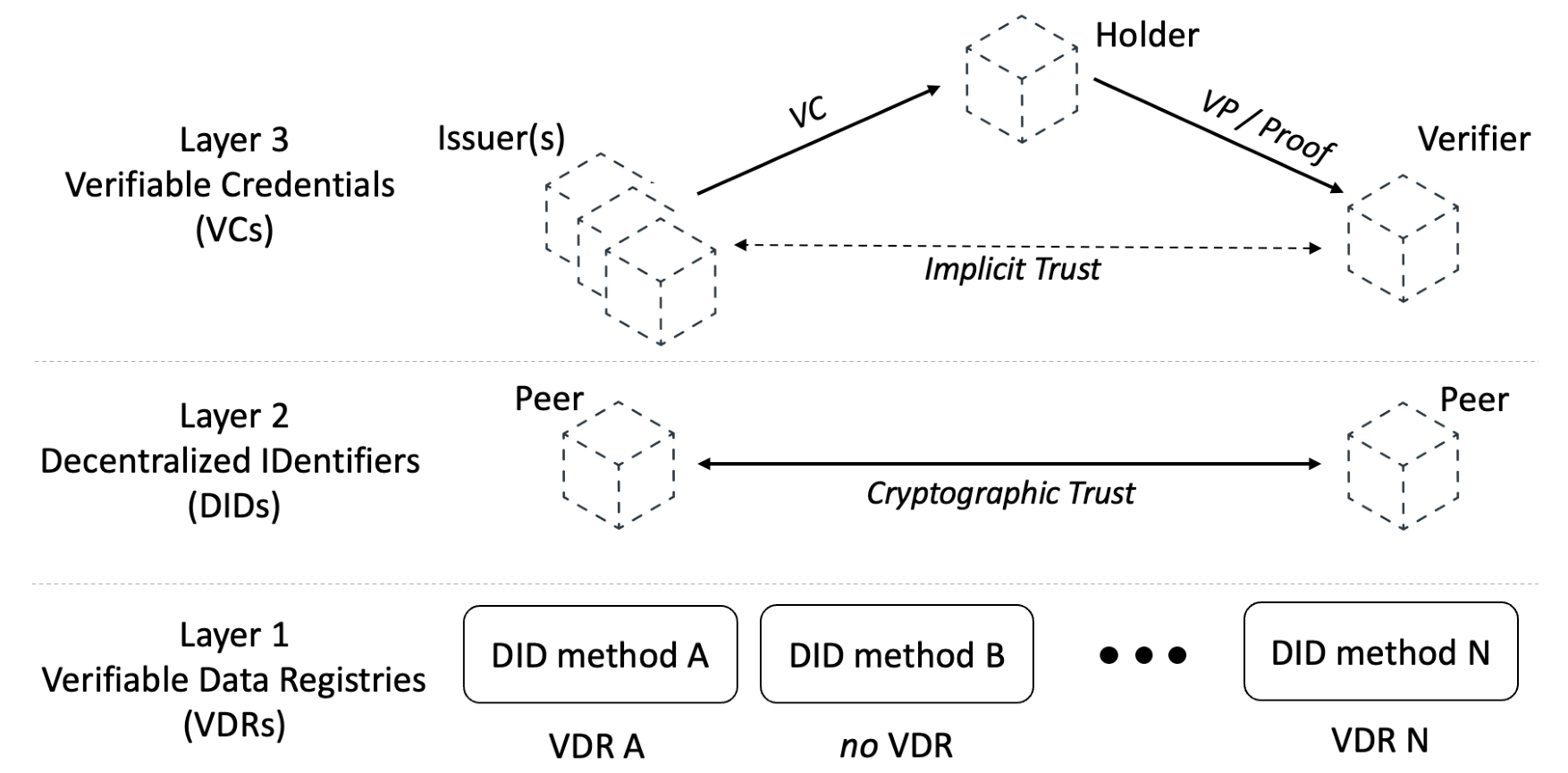
Figure 1: The Self-Sovereign Identity reference model. Source [13].
Layer 3 works according to the so-called Triangle of Trust (ToT), which consists of three entities:
- The Issuer of the VC (e.g., the government or a private company) is the entity that creates and signs the verifiable credential, ensuring the credential’s credibility and authenticity.
- The Holder of the VC is the entity (an individual or an organization) that can generate Verifiable Presentations (VPs) to prove its Claims (e.g., age of majority, driving license, subscription to a service).
- The Verifier is the entity that receives and checks the VPs of the Holder.
A credential system based on plaintext VCs does not protect the privacy of the Holder because the VC, the claims in the VP, and the digital signature of the Issuer are exchanged in plain text. In particular, plaintext VCs result in the linkability and traceability of peers.
Anonymous VCs (also known as Zero-Knowledge VCs) represent a privacy-preserving alternative that enables the Holder to manage its VCs by choosing the level of information disclosure. For anonymous VCs, the roles in the ToT are modified as follows.
- The Issuer asserts the capability of a Holder to prove its identity, possibly based on the knowledge of some secret attributes. After proper verification, the Issuer issues the anonymous VC to the Holder.
- The Holder owns the anonymous VC and can take advantage of zero-knowledge cryptographic primitives and protocols to interact with the Issuer and Verifier in a privacy-preserving way. This means that the Holder can obtain a VC and prove that its identity satisfies certain properties while still maintaining the desired level of privacy. These operations can happen in a completely anonymous way (i.e., without revealing any identity details) or by selectively disclosing only a subset of the claims contained in the VC (i.e., without revealing specific secret attributes). The Holder can prove, via a VP, to the Verifier that its VC is legitimate, which means it contains a valid signature generated by an Issuer, known as the Proof of Knowledge of a Signature (PoKS).
- The Verifier receives a PoKS from the Holder and verifies that the Holder actually holds a valid VC, containing the undisclosed secrets and a valid signature from an Issuer.
Post-Quantum Verifiable Credentials
QUBIP is implementing post-quantum plaintext VCs (with both a pure post-quantum and a post-quantum/traditional hybrid approach) and post-quantum anonymous VCs with selective disclosure capabilities. This transition exercise employs the IOTA Identity library [2], which is a widely used SSI library written in Rust and is the result of a large open-source, community-led SSI project maintained by the IOTA Foundation. This library provides all the functionality to handle W3C-compliant DIDs, DID documents, VCs, and VPs. In essence, it is a general-purpose SSI library, and therefore the perfect target for a transition exercise.
Plaintext VCs
The main cryptographic technologies in SSI with plaintext VCs are traditional public-key digital signature schemes. These are based on cryptographic assumptions, such as the hardness of the factorization problem and the discrete logarithm problem, which no longer hold in the presence of (sufficiently powerful) quantum computers capable of running Shor’s algorithm. Therefore, the transition to post-quantum plaintext VCs, while technically challenging, is conceptually easy: it mostly involves replacing traditional public-key digital signature schemes with their post-quantum counterparts. Specifically, QUBIP is transitioning plaintext VCs to post-quantum by employing the digital signature schemes of the Module-Lattice-Based Digital Signature Standard (ML-DSA), which is close to final standardization, thus ensuring both current security requirements and timely implementation of the project [3].
Anonymous VCs
As for plaintext VCs, anonymous VCs based on traditional cryptography, such as CL [4] or BBS [5], are primarily based on the assumption of the hardness of the discrete logarithm problem, making them unsuitable for the post-quantum world. However, in contrast to plaintext VCs, transitioning anonymous VCs to the post-quantum world is significantly more complex.
Indeed, as we mentioned before, anonymous VCs require a mechanism for a PoKS. A PoKS, in turn, usually consists of two parts: a “signature scheme with efficient protocols” (informally, a digital signature scheme with specific features such as the ability to sign committed hidden messages and to prove knowledge of a signature on such messages) and an associated zero-knowledge proof system. While there are many practical proposals for post-quantum zero-knowledge proof systems, the state of post-quantum “signature schemes with efficient protocols” is still at the frontier of research.
First, post-quantum anonymous VCs have been proposed only recently (not before 2022) [6, 7, 8, 9], with the exception of the proposal of Libert et al. [10], which is however impractical due to having a signature size of at least 670 MB [6, p. 4]. Second, the literature on post-quantum anonymous VCs is quite scarce, essentially only the aforementioned papers. Third, none of the papers introducing these schemes is accompanied by a software implementation, nor does any of them take into account implementation issues such as performance and protection against side-channel attacks.
The four proposed schemes [10, 6, 7, 8] are all based on lattice assumptions. The first three represent sequential improvements on each other, with proof sizes steadily decreasing—from 670 MB in [10], to 640 kB in [6], and finally to 500 kB in [7].
The fourth scheme [8], authored by Bootle, Lyubashevsky, Nguyen, and Sorniotti, takes a different approach from the previous proposals. This scheme, which we refer to as the “BLNS framework”, provides the shortest credentials yet, with a size of around 125 kB. In addition to its compactness, the BLNS framework has strong security properties. Specifically, even if the Issuer and Verifier are malicious and collaborate, the process of issuing and verifying a set of attributes reveals no information about the Holder’s non-disclosed attributes. Additionally, the scheme guarantees that malicious Holders cannot generate valid VPs for attributes that were not originally issued by the Issuer, even in scenarios of collusion.
For transitioning anonymous VCs into the post-quantum era, QUBIP has chosen the BLNS framework. This selection is due to its small proof size, maturity in terms of implementability (the paper provides several pages of pseudocode), and security properties tailored for web applications.
BLNS is based on the hardness of a family of lattice problems called , which is parameterized by a function , where ISIS stands for Inhomogeneous Shortest Integer Solution. The problem is too technical to be stated here in its entirety. However, roughly speaking, given a random matrix and access to an oracle that chooses a random and returns , where is a short vector such that , the task is to produce a pair , where , is a short vector with , and has not been previously outputed by the oracle.
The problem has not been considered in previous schemes, but it is a very natural generalization of the underlying problem upon which the classic GPV signature scheme is based [11], and it is also similar to other recently and independently proposed lattice assumptions [12]. Furthermore, when the function is modeled as a random oracle and is chosen from a distribution with enough entropy, the problem becomes equivalent to the well-known and lattice problems.
In the concrete instantiation of in the BLNS framework, is chosen as a linear function of the binary representation of the input . At first glance, this might seem like a bad choice, since linearity appears to be exploitable. However, upon further consideration, the condition that must be a short vector prevents such exploitation (essentially because the sum of random binary vectors is not a binary vector, except with negligible probability).
References
[1] M. Sporny, D. Longley, and D. Chadwick. Verifiable Credentials Data Model v2.0, August 2023. https://www.w3.org/TR/vc-data-model-2.0.
[2] IOTA Foundation. IOTA Identity library, 2024.
[3] NIST. FIPS 204, Module-Lattice-Based Digital Signature Standard, 2023.
[4] J. Camenisch and A. Lysyanskaya. A signature scheme with efficient protocols. In Security in Communication Networks, pages 268–289, Amalfi (IT), September 2002.
[5] J. Camenisch, M. Drijvers, and A. Lehmann. Anonymous attestation using the strong Diffie-Hellman assumption revisited. In TRUST-2016 – 9th Int. Conf. on Trust and Trustworthy Computing, pages 1–20, Vienna (AT), August 2016.
[6] C. Jeudy, A. Roux-Langlois, and O. Sanders. Lattice signature with efficient protocols, application to anonymous credentials. IACR Cryptology ePrint Archive, Paper 2022/509, 2022. https://eprint.iacr.org/2022/509.
[7] Q. Lai, C. Chen, F.-H. Liu, A. Lysyanskaya, and Z. Wang. Lattice-based commit-transferrable signatures and applications to anonymous credentials. IACR Cryptology ePrint Archive, Paper 2023/766, 2023. https://eprint.iacr.org/2023/766.
[8] J. Bootle, V. Lyubashevsky, N. K. Nguyen, and A. Sorniotti. A framework for practical anonymous credentials from lattices. IACR Cryptology ePrint Archive, Paper 2023/560, 2023. https://eprint.iacr.org/2023/560.
[9] J. Bootle, V. Lyubashevsky, N. K. Nguyen, and A. Sorniotti. A framework for practical anonymous credentials from lattices. In CRYPTO 2023, pages 384–417, Santa Barbara (CA, USA), August 2023.
[10] B. Libert, S. Ling, F. Mouhartem, K. Nguyen, and H. Wang. Signature schemes with efficient protocols and dynamic group signatures from lattice assumptions. In ASIACRYPT 2016, pages 373–403, Hanoi (VN), December 2016.
[11] C. Gentry, C. Peikert, and V. Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. Cryptology ePrint Archive, Paper 2007/432, 2007. https://eprint.iacr.org/2007/432.
[12] M. R. Albrecht, V. Cini, R. W. F. Lai, G. Malavolta, and Sri AravindaKrishnan Thyagarajan. Lattice-based SNARKs: Publicly verifiable, preprocessing, and recursively composable. Cryptology ePrint Archive, Paper 2022/941, 2022. https://eprint.iacr.org/2022/941.
[13] A. Pino, D. Margaria, A. Vesco. On PQ/T Hybrid Verifiable Credentials and Presentations to Build Trust in IoT Systems. In Proceedings of 9th International Conference on Smart and Sustainable Technologies (SpliTech), pages 1-6, Bol and Split, Croatia: IEEE, June 2024. DOI 10.23919/SpliTech61897.2024.10612295.
